Är du i skolan just nu? 

KitAmetam: Du tar ett lån på 20000 kr, som du ska betala tillbaka efter 3 år. Varje kvartal läggs räntan till skulden. Hur stor är din skuld efter 3 år om räntesatsen hela tiden är 5,95% per kvartal?

A är vad du betalar varje kvartal, ta detta antal multiplicerat med antal gånger du ska betala ( 3 år x 4 ggr per år = totalt 12 ggr) och du får det totala beloppet. Det finns säkert enklare sätt att räkna men jag orkar inte tänka mer.

Alltså:
Tot skuld = A x 12
A beräknas enligt formeln nedan.
----------------------------------------------------------------------------------------------------

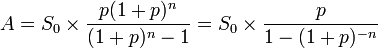
För att beräkna annuiteten (A) behövs:

• S0 = Lånebelopp. Skuld vid löptidens början.
• p = Räntesats för perioden. En årsränta måste delas med antalet betalningsperioder per år (12 för månader, 4 för kvartal, etc). En årsränta på 9% ger alltså en månatlig räntesats på 0,0075 (=0,75% = 9%/12).
• n = Antal betalningar under lånets löptid. Månatlig amortering ger 60 (=12*5) betalningar för ett lån på fem år.

-------------------------------------------------------------------------------------------------------

Räkna först ut hur många kvartal 3 år är. Sedan dividerar du skulden på antalet kvartal (antar att man ska amortera samma summa varje kvartal). Efter det räknar du ut årliga räntan och dividerar med 4 (för att få det till ett kvartal) och adderar det till amorteringen. Sedan inför nästa kvartal räknar du ut räntan genom att subtrahera det du redan betalt från skulden, och räknar ut räntan för det kvartalet och adderar det till amorteringen. Lättast om man gör en tabell.

MarcusKing:
Är du i skolan just nu? 

Nej, har lov men slipper inte läxor för det 

KitAmetam:

Nej, har lov men slipper inte läxor för det 

Det slipper jag 

typ 26% i effektiv årsränta, lär de ut att amortera på sms-lån i skolan nu för tiden, eller?

player one: typ 26% i effektiv årsränta, lär de ut att amortera på sms-lån i skolan nu för tiden, eller?

Hur får du fram den siffran?

Razor: Hur får du fram den siffran?

x*1,0595*1,0595*1,0595*1,0595. då räknar jag med ränta på ränta-effekt, och formulerar man lånet som att räntan räknas för varje kvartal så får jag anta att den effekten gäller mellan kvartal också.

player one: x*1,0595*1,0595*1,0595*1,0595. då räknar jag med ränta på ränta-effekt, och formulerar man lånet som att räntan räknas för varje kvartal så får jag anta att den effekten gäller mellan kvartal också.

Ja just det, tankevurpa...

Razor:

Ja just det, tankevurpa...

KitAmetam: Uppgift

Lösning

(20000×(1+5,95/100)^(3×4)) kr=(20000×(1+0,0595)¹²) kr=(20000×1,0595¹²) kr≈40017 kr

AndersLkpg: Lösning(20000×(1+5,95/100)^(3×4)) kr=(20000×(1+0,0595)¹²) kr=(20000×1,0595¹²) kr≈40017 kr

Jaha, var återbetalningen tänkt att ske på en gång utan amortering?

Razor: Jaha, var återbetalningen tänkt att ske på en gång utan amortering?

Jag har antagit att detta är en rimlig tolkning av uppgiften, då det inte står något i uppgiftens text om att någon typ av amortering ska förekomma.