Som titeln lyder. Om man vet att en trubbig triangel: ABC är vinkeln A: 42grader. sidan AB är 10 cm. sidan Bc är 9 cm. Hur gör man för att lösa ut den största vinkeln C?
Man använder trigonometri tror jag.
Uppgift
Enheter
cm
grader
Förutsättningar
A+B+C=180
sin(A)/BC=sin(B)/AC=sin(C)/AB
0<A<180
0<B<180
90<C<180
-90≤arcsin(x)≤90, -1≤x≤1
A=42
AB=10
BC=9
Lösning
sin(A)/BC=sin(C)/AB
ABsin(A)/BC=sin(C)
sin(C)=ABsin(A)/BC
C[1]=arcsin(ABsin(A)/BC)
C[2]=180-arcsin(ABsin(A)/BC)
-90≤arcsin(ABsin(A)/BC)≤90
-90≤C[1]≤90
-90≤C≤90
Omöjligt
-90≤-arcsin(ABsin(A)/BC)≤90
180-90≤180-arcsin(ABsin(A)/BC)≤180+90
90≤180-arcsin(ABsin(A)/BC)≤270
90≤C[2]≤270
90≤C≤270
90<C<180
Möjligt
C=C[2]
C=180-arcsin(ABsin(A)/BC)
C=180-arcsin(10sin(42)/9)
C≈132
Svar
Vinkeln C är ungefär 132 grader.
Länkar
http://sv.wikipedia.org/wiki/Sinussatsen
http://sv.wikipedia.org/wiki/Trigonometrisk_funktion#Inversa_funktioner
Uppgift
Enheter
cm
grader
Förutsättningar
A+B+C=180
sin(A)/BC=sin(B)/AC=sin(C)/AB
0<A<180
0<B<180
90<C<180
-90≤arcsin(x)≤90, -1≤x≤1
A=42
AB=10
BC=9
Lösning
sin(A)/BC=sin(C)/AB
ABsin(A)/BC=sin(C)
sin(C)=ABsin(A)/BC
C[1]=arcsin(ABsin(A)/BC)
C[2]=180-arcsin(ABsin(A)/BC)
-90≤arcsin(ABsin(A)/BC)≤90
-90≤C[1]≤90
-90≤C≤90
Omöjligt
-90≤-arcsin(ABsin(A)/BC)≤90
180-90≤180-arcsin(ABsin(A)/BC)≤180+90
90≤180-arcsin(ABsin(A)/BC)≤270
90≤C[2]≤270
90≤C≤270
90<C<180
Möjligt
C=C[2]
C=180-arcsin(ABsin(A)/BC)
C=180-arcsin(10sin(42)/9)
C≈132
Svar
Vinkeln C är ungefär 132 grader.
Länkar
http://sv.wikipedia.org/wiki/Sinussatsen
http://sv.wikipedia.org/wiki/Trigonometrisk_funktion#Inversa_funktioner
AndersLkpg: Vinkeln C är ungefär 132 grader.
varför fick jag det till 101 grader? Vad gjorde jag för fel?
AndersLkpg: Vinkeln C är ungefär 132 grader.
Jag gjorde 9*sin 42/10Sedan tog jag 180-42- arc sin 9*sin42/10. Gjorde jag fel?
AndersLkpg: Vinkeln C är ungefär 132 grader.
Tex här:
I en trubbigt vinklad tringel så är sidan a = 12 cm, sidan c = 13 cm and vinkeln A = 60°. Finn vinkeln C, sidan b och arean till triangeln.
Detta är samma exempel som ovan förutom att en vinkel i triangeln är trubbig ( större än 90°).
När vi fann vinkeln C i exempel1 ovan så antog vi att räknaren gav oss det rätta svaret. Beräkningarna var som följer:
[img border="0" src="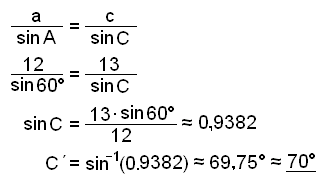 
" width="322" height="182">sinC = 0,9382
Vi får redan på att denna triangel har en trubbig vinkel så vi måste komma ihåg regeln som ger oss den andra lösningen till ekvationen. Denna regel är:
sin v° = sin (180° − v°)
Detta ger oss den trubbiga vinkeln C ≈ 180° − 70° ≈ 110° och därför är vinkeln B ≈ 180° − 60° − 110° ≈ 10°
länk: http://www.rasmus.is/sv/t/G/Su55k03.htm exempel 2
AndersLkpg: Vinkeln C är ungefär 132 grader.
kan man fortfarande få något poäng på de sättet jag gjorde?
